Peter Mark Roget
“Explanation of an Optical Deception in the Appearance of the Spokes of a Wheel seen through Vertical Apertures.”
(Read December 9, 1824, later published in the ‘Philosophical Transactions of the Royal Society’, London, 1825)
A curious optical deception takes place when a carriage wheel, rolling along the ground, is viewed through the intervals of a series of vertical bars, such as those of a palisade, or of a Venetian window-blind. Under these circumstances the spokes of the wheel, instead of appearing straight, as they would naturally do if no bars intervened, seem to have a considerable degree of curvature. The distinctness of this appearance is influenced by several circumstances presently to be noticed; but when every thing concurs to favour it, the illusion is irresistible, and, from the difficulty of detecting its real cause, is exceedingly striking.
The degree of curvature in each spoke varies according to the situation it occupies for the moment with respect to the perpendicular. The two spokes which arrive at the vertical position, above and below the axle, are seen of their natural shape, that is, without any curvature. Those on each side of the upper one appear slightly curved; those more remote, still more so; and the curvature of the spokes increases as we follow them downwards on each side till we arrive at the lowest spoke, which, like the first, again appears straight.
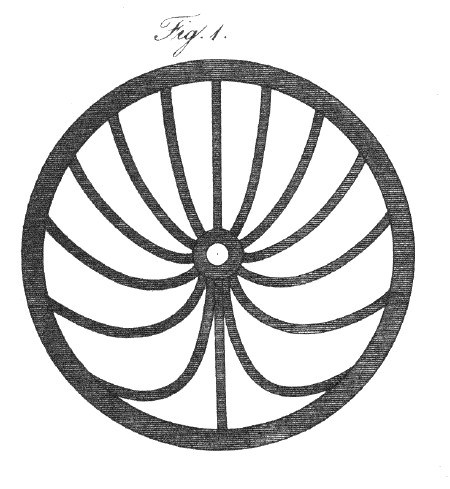
The most remarkable circumstance relating to this visual deception is, that the convexity of these curved images of the spokes is always turned downwards, on both sides of the wheel; and that this direction of their curvature is precisely the same, whether the wheel be moving to the right or to the left of the spectator. The appearance now described is represented in Plate XI. fig. 1.*
(note: The appearance in question has been noticed by an anonymous writer in the Quarterly journal of Science (Vol. X. p. 2,82) who gives, however, no explanation of the phenomenon. It would have been impossible, indeed, to reconcile the facts as they are there stated, with any theory that could be imagined for their solution.)
In order to discover a clue to the explanation of this phe-nomenon, it was necessary to observe the influence which certain variations of circumstances might have upon it; and the following are the principal results of the experiments I made for this purpose.
1. A certain degree of velocity in the wheel is necessary to produce the deception above described. If this velocity be gradually communicated, the appearance,of curvature is first perceptible in the spokes which have a horizontal position: and as soon as this is observed, a small increase given to the velocity of the wheel, produces suddenly the appearance. of curvature in all the lateral spokes. The degree of curvature remains precisely the same as at first, whatever greater velocity be given to the wheel, provided it be not so great as to prevent the eye from following the spokes distinctly as they revolve: for it is evident, that the rapidity of revolution may be such as to render the spokes invisible. It is also to be noticed that, however rapidly the wheel revolves, each individual spoke appears, during the moment it is viewed, to be at rest.
2. The number of spokes in the wheel makes no difference in the degree of curvature they exhibit.
3. The appearance of curvature is more perfectly seen when the intervals between the bars through which the wheel is viewed, are narrow ; provided they are sufficiently wide to allow of the distinct view of all the parts of the wheel in succession, as it passes along. For the same reason, the phenomenon is seen to the greatest advantage when the bars are of a dark colour, or shaded, and when a strong light is thrown upon the wheel. The deception is, in like manner, aided by every circumstance which tends to abstract the attention from the bars, and to fix it upon the wheel.
4. If the numbers of bars be increased in the same given space, no other difference will result than a greater multiplication of the curved images of the spokes; but if a certain relation be preserved between the angles subtended at the eye by the whole intervals of the bars, and of the extremities of the spokes, this multiplication of images may be corrected. The distance of the wheel from the bars is of no consequence, unless the latter are very near the eye, as in that case the apertures between them may allow too large a portion of the wheel to be seen at once.
5. If the bars, instead of being vertical, are inclined to the horizon, the same general appearances result; but with this difference that the spokes occupying positions parallel to the bars, are those which have no apparent curvature : while the curvatures of the other spokes bear the same relations to these straight spokes, and to each other, that they did in. the former case. When the inclination of the bars is considerable, however, the images become more crowded, and the distinctness of the appearance is thereby diminished. The deception totally ceases when the wheel is viewed through bars that are parallel to the line of its motion.
6. It is essential to the production of this effect, that a combination should take place of a progressive with a rotatory motion. Thus, it will not take place if, when the bars are stationary, the wheel simply revolves on its axis, without at the same time advancing: nor when it simply moves horizontally, without revolving. On the other hand, if a progressive motion be given to the bars, while the wheel revolves round a fixed axis, the spokes immediately assume a curved appearance. The same effect will also result if the revolving wheel be viewed through fixed bars by a spectator, who is himself moving either to the right or left; because such a movement on the part of the spectator produces in his field of vision an alteration in the relative situation of the bars and wheel.
It is evident from the facts above stated, that the deception in the appearance of the spokes must arise from the circumstance of separate parts only of each spoke being seen at the same moment; the remaining parts being concealed from view by the bars. Yet since several parts of the same spoke are actually seen in a straight line through the successive apertures, it is not so easy to understand why they do not connect themselves in the imagination, as in other cases of broken lines, so as to convey the impression of a straight spoke. The idea at first suggests itself that the portions of one spoke, thus seen separately, might possibly connect themselves with portions of the two adjoining spokes, and so on, forming by their union a curved image made up of parts from different successive spokes. But a little attention to the phenomena will show that such a solution cannot apply to them: for when the disc of the wheel, instead of being marked by a number of radiant lines, has only one radius marked upon it, it presents the appearance, when rolled behind the bars, of a number of radii, each having the curvature corresponding to its situation; their number being determined by that of the bars which intervene between the wheel and the eye. So that it is evident, that the several portions of one and the same line, seen through the intervals of the bars, form on the retina the images of so many different radii.
The true principle, then, on which this phenomenon depends, is the same as that to which is referable the illusion that occurs when a bright object is wheeled rapidly round in a circle, giving rise to the appearance of a line of light throughout the whole circumference: namely, that an impression made by a pencil of rays on the retina, if sufficiently vivid, will remain for a certain time after the cause has ceased. Many analogous facts have been observed with regard to the other senses, which, as they are well known, it is needless here to particularize.
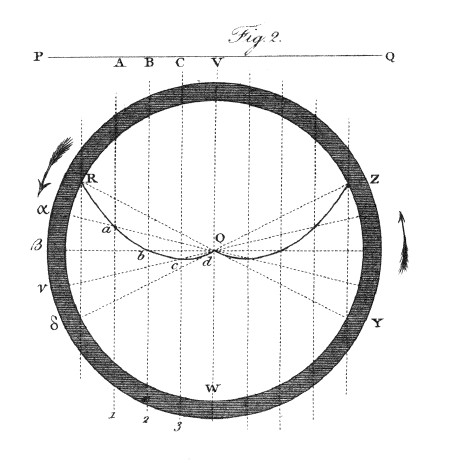
In order to trace more distinctly the operation of this principle in the present case, it will be best to take the phenomenon in its simplest form, as resulting from the view of a single radius, (fig. 2.) OR of the wheel VW, revolving steadily upon its axis, but without any progressive motion, and seen through a single narrow vertical aperture which is moving horizontally in a given direction PQ. Let us also assume that the progressive motion of the aperture is just equal to the rotatory motion of the circumference of the wheel. It is obvious that if, at the time of the transit of the aperture, the radius should happen to occupy either of the vertical positions VO or OW, the whole of it would be seen at once through the aperture, in its natural position; but if, while descending in the direction VR, it should happen to be in an oblique position RO, terminating at any point of the circumference at the moment the aperture has, in its progress horizontally, also arrived at the same point R, the extremity of the radius will now first come into view, while all the remaining part of it is hid. By continuing to trace the parts of the radius that are successively seen by the combined motions of the aperture and of the radius, we shall find that they occupy a curve Rabcd generated by the continued intersection of these two lines. Thus, when the aperture has moved to A. the radius will be in the position O-alpha; when the former is at B, the latter will be at 0-beta, and so on.
Again; let us suppose that when the aperture is just passing the centre, the radius should be found in a certain position on the other side OY, and rising towards the summit. Then tracing, as before, the intersections of these lines in their progress, we shall obtain a curve precisely similar to the former. Its position will be reversed; but its convexity will still be downwards.
If the impressions made by these limited portions of the several spokes follow one another with sufficient rapidity, they will, as in the case of the luminous circle already alluded to, leave in the eye the trace of a continuous curve line and the spokes will appear to be curved, instead of straight.
The theory now advanced is in perfect accordance with all the phenomena already detailed, and is farther confirmed by extending the experiments to more complicated combinations.
It readily explains why the image, or spectrum, as it may be called, of the spoke, is at rest, although the spoke itself be revolving: a circumstance which might escape notice, if the attention were not particularly called to it.
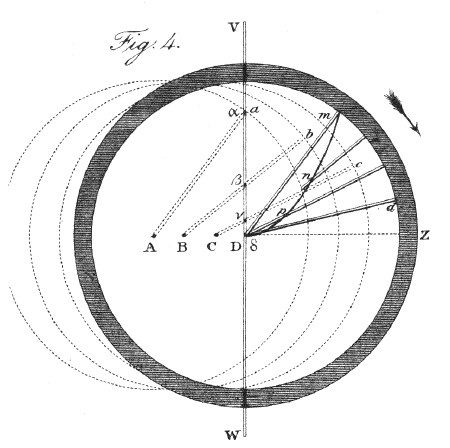
Since the curved appearance of the lines results from the combination of a rotatory, with a progressive motion of the spokes, in relation to the apertures through which they are viewed, it is evident that the same phenomena must be produced if the bars be at rest, and both kinds of motion be united in the wheel itself. For, whether the bars move horizontally with respect to the wheel, or the wheel with respect to the bars, the relative motion between them, and its effects, in as far as concerns the appearance in question, must be the same. The attention of the spectator should in both cases be wholly directed to the wheel, so that the motions in question should be referred altogether to it. Thus, in fig. 4, the real positions, at successive intervals of time, of the spoke Aa, when the wheel is rolling on the ground in the direction AZ, are expressed by the lines Aa, Bb, Cc and Dd. While the spoke is in these positions, the portions of it really seen through the fixed aperture VW, are the parts , alpha, beta, gamma, delta, the impressions of which, being retained upon the retina, and referred to the wheel when in its last position, form the series of points m, n, p and q, in the curved spectrum m D.
That the attention may the more easily follow the wheel in its progression, it is necessary that its circumference be distinctly seen, and its real situation correctly estimated. Hence, although it be true, that by a sufficient exertion of attention the phenomenon may be exhibited by means of a single aperture, it is much more readily perceived, when the number of apertures is such as to allow the wheel to be seen in its whole progress. For this reason the phenomenon is very distinct in the case of a palisade. Each aperture produces its own system of spectra; and hence, when the apertures occur at short intervals, the number of the spokes is considerably multiplied; but if the intervals be so adjusted as to correspond with the distances between the spokes at the circumference of the wheel, the images produced by each aperture will coalesce, and the effect will be much heightened.
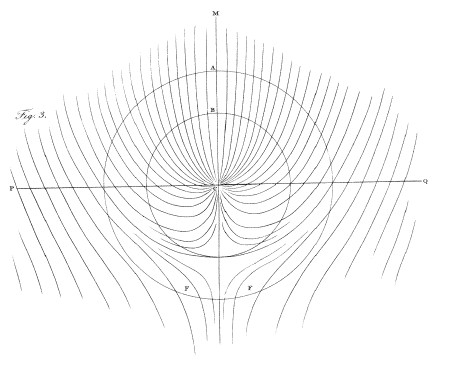
A mathematical investigation of the curves resulting from the motion of the points of intersection of a line moving parallel to itself, with another line revolving round its axis, will show them to belong to the class of QUADRATRICES, of which the one which touches the circumference of the inner generating circle is that which is known by the name of the QUADRATRIX OF, DINOSTRATES. Such a system of curves is represented in fig. 3, where MC, CN are the generating radii, A the outer, and B the inner generating circles, and PQ the common axis of the curves.
All these curves have the same general equation, namely
y = (b – x). tang. x.
where the co-ordinates are referred to the axis at right angles to the vertical generating radii, and passing through the centre of their revolution: the basis b being measured on the axis from the point of its intersection with the curve to the centre: and x being the arc of the inner generating circle, as well as the abscissa.*
(note: This equality between the arc and the abscissa is a necessary consequence of the progressive motion of the wheel being equal to the rotatory motion of its circumference : the former motion producing the increments of the abscissa; and the latter those of the arc of the circle. The equation y = (b – x). tang. x. is deduced from a simple analogy of the sides of similar triangles.) A wheel simply rolling on its circumference exhibits, when seen through fixed bars, only those portions of the curves which are contained within the inner circle; but when its motion of revolution is more rapid than its horizontal progression, as when it is made to roll on an axle of less diameter on a raised rail-way, then the remaining portions of the curves will be seen, and others, on the lower part of the wheel, having a contrary flexure, will also make their appearance. These are seen at FF in fig. 3.
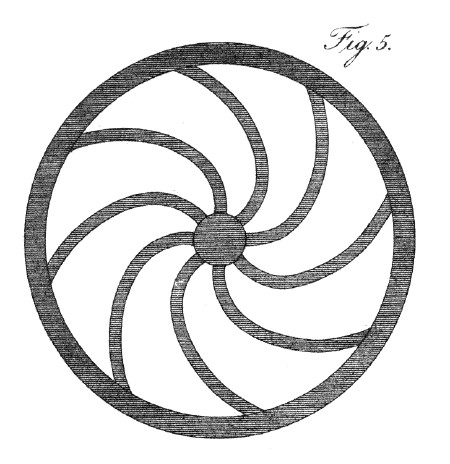
If the spokes, instead of being straight, be already curved, like those of the Persian water-wheel, their form, when viewed through bars, will undergo modifications, which may readily be traced by applying to them the same theory. Thus, by giving a certain curvature to the spokes, as in fig. 5, they will at one part of their revolution appear straight, namely, where the optical deception operates in a direction contrary to the curvature. The velocity of the apparent motion of the visible portions of the spokes is proportionate to the velocity of the wheel itself; but it varies in different parts of the curve: and might therefore, if accurately estimated, furnish new modes of measuring the duration of the impressions of light on the retina.